Research purpose: This article challenged the assumption that most financial time series are first differenced stationary. The common difference first, ask questions later approach was revisited by taking a more systematic approach when analysing the statistical properties of financial time series data.

Motivation for the study: Since Nelson and Plosser’s (1982) argued that many macroeconomic time series are difference stationary, many econometricians simply differenced data in order to achieve stationarity. However, the inherent properties of time series data have changed over the past 30 years. This necessitates a proper evaluation of the properties of data before deciding on the appropriate course of action, in order to avoid over-differencing which causes variables to lose their explanatory ability that leads to spurious results.

Research approach, design and method: This article introduced a rigorous process that enables econometricians to determine the most appropriate form of stationarity, which is led by the underlying statistical properties of several financial and economic variables.

Main findings: The results highlighted the importance of consulting the d parameter to make a more informed decision, rather than only assuming that the data are I(1). Evidence also suggested that the appropriate form of stationarity can vary, but emphasises the importance to consider a series to be fractionally differenced.

Practical/managerial implications: Only when data are correctly classified and transformed accordingly will the data be neither under- nor over-differenced, thus enhancing the validity of the results generated by statistical models.

Contribution/value-add: By utilising this rigorous process, econometricians will be able to generate more accurate out-of-sample forecasts, as already proven by Van Greunen, Heymans, Van Heerden and Van Vuuren (2014).

Capturing and examining the properties of financial time series, therefore, require that univariate financial time series are stationary before they are examined. Since the majority of financial time series data are likely to be non-stationary in their raw form, it is necessary to transform these time series in some manner to obtain a stationary series before further economic modelling can continue. In order to ensure that errors are not auto-correlated, Granger and Newbold (1974) suggest that the individual data series be differenced and that these stationary series be used for linear regression purposes. It is this line of research, together with the work of Nelson and Plosser (1982), which argued that many macroeconomic time series are difference stationary and not trend stationary, that led to the common practice of transforming non-stationary data by means of the first difference approach. Also, the complexity of alternative fractional differencing methods forced economists and financial analysts to use only first differencing and log differencing to render a time series stationary (Erfani & Samimi 2009). Unfortunately these practices can, and often do, lead to over-differencing. When data are over-differenced the variance of these time series is larger than that of the original MA(1) series. This is obviously an issue, especially when dealing with autoregressive moving average type models (Xiu & Jin 2007). The finer nuances of the data are also reduced by over-differencing, thus reducing the explanatory power of what remains (Plosser & Schwert 1977).

Although it is important to get data stationary before attempting any linear regression analysis, both under-differencing and over-differencing will lead to sub-optimal results. The literature has, however, focused so much on the negative aspects of under-differencing that data have been over-differenced in many studies in an attempt to ensure that spurious results are eliminated. Although the authors agree with the results found by Nelson and Plosser (1982), we challenge this belief three decades later. The properties of financial time series data have changed tremendously over the last two decades alone. Events such as the introduction of the Euro as accounting currency in 1999 for example have led to a fundamental shift in the dynamics of several European countries’ interest rate data (Bekaert et al. 2013). Other events led to an increase in volatility in economic and financial time series data. These include the announcement of North Korea’s nuclear intensions (October 2006), the commodity crisis that caused the dramatic increase of metal and energy prices (from 2007 to 2008) and the effects of the 2008 global financial crisis.

It is therefore necessary to revisit the issue of stationarity in order to establish an unambiguous method to determine the appropriate form of stationarity for both economic and financial time series data. In order to achieve this objective this article will commence with an overview of the models available to test for stationarity (Section 2). A structured process will then be introduced in Section 3 that will enable an econometrician to determine the appropriate form of stationarity (see also Figure 1A). This process should be viewed as a set of action steps to be taken to ensure that the data is neither over-differenced nor under-differenced. The empirical results will be reported in Section 4, followed by the concluding remarks and recommendations in Section 5.

There are also several tests for testing stationarity with stationarity as the null hypothesis; these include the KPSS test (after Kwaitkowski et al. 1992), the Dickey-Fuller Generalised Least Squares (DF-GLS) test as well as tests by Tanaka (1990), Park (1990), Saikkonen and Luukkonen (1993), Choi (1994), Leybourne and McCabe (1994; 1996) and Arellano and Pentula (1995). However, in an attempt to establish a less complex unambiguous method to determine the appropriate form of stationarity, this article will only make use of the ADF, KPSS and DF-GLS tests to construct a formalised process of rendering non-stationary data stationary.

In the past, unit root tests such as the PP and ADF tests have been criticised for their lack of power in determining the presence of unit roots. Blough (1992) for example warns that no test can have high power against any stationary process without a correspondingly high probability of falsely rejecting nearby members of the unit root null. This means that such tests are not able to maintain a nominal level over all members of the null space, whilst displaying high power against at least some alternatives. This leads to the conundrum that these tests often cannot distinguish between true unit root processes, where δ = 0, and near unit root processes where δ is only close to zero.

This issue arises more often when working with data frequencies greater than quarterly, thus making them less useful in these circumstances (Maddala & Kim 2000). This poses a problem for the econometrician analysing financial time series data that tend to be either weekly, daily or intra-day data. However, Kwaitkowski et al. (1992) and Choi (1994) argue that it is preferable to use a combination of tests, testing for both a unit root and for stationarity as the null hypothesis, where the KPSS tests must be used as a confirmatory analysis to that of the ADF tests (Maddala & Kim 2000). Also, the complexity to determine fractional unit roots poses a further problem for researchers aiming to determine whether a time series is fractionally differenced stationary. To overcome these shortcomings a formalised process is introduced in order to overcome the problem of possibly over-differencing the data and stripping it of descriptive properties. This process will be discussed in the following section.

The process proposed here of determining the appropriate form of stationarity consists of three phases (graphically depicted in Figure 1A). The first phase entails determining the presence of a unit root as well as the order of integration. Phase two continues by testing for stationarity as the null hypothesis and determines the presence of a possible deterministic trend in the data. The final phase determines the possibility of fractional integration and includes the final evaluation procedure to determine the correct approach to render a time series stationary.

These regression equations are similar, except for the presence of an intercept term in Equation 2, and an intercept and trend term in Equation 3. The central focus point of all three equations is γ where γ = 0 indicates that the time series contains a unit root (Asteriou & Hall 2007; Enders 2010). In the unlikely event of a white noise error term, Dickey and Fuller extended the DF test to include extra lagged terms of the explanatory variable (Asteriou & Hall 2007). This extended version is known as the ADF test and the inclusion of extra lagged dependent variables eliminates the presence of autocorrelation. The ADF follows on the three different forms used in the DF test and can be performed using the following three regressions:

Asteriou and Hall (2007) explain a three-step method for using the ADF tests for unit roots with the aim of concluding that a series is stationary. The first is to test the time series for a unit root and, if none exists, the time series is stationary and is classified I(0), otherwise it contains a unit root and is classified I(n). The second step is to take first differences (in cases where a unit root is present) and test the first differenced series for a unit root; if there is none, the data series is stationary and is classified I(1), otherwise it contains a unit root and is classified I(n). The first difference of a process refers to the change within the process from one time period to the next (Burke & Hunter 2005). The first difference of a time series x_t is, therefore, x^t – x^t–1 and is denoted by ∆x^t. It then follows that ∆x^t = ε^t with ε^t assumed to be a white noise process and ∆x^t therefore being a stationary process (Burke & Hunter 2005). The third step entails differencing the time series up to the point where the tests indicate no presence of a unit root. This implies that it is also possible to take the second difference of a time series, that is ∆²x^t = ∆ε^t by repeating the same process. But, if a time series that is I(1) is second differenced, the time series might be over-differenced, so care should be taken that a time series is only differenced the minimal number of times needed to render the series stationary (Burke & Hunter 2005).

After establishing the order of integration with the ADF test, it is important to confirm these results with additional tests. This leads to the next phase that will test for the presence of stationarity as the null hypothesis and the possible presence of a deterministic trend as the reason for the non-stationarity of a time series.

In Equation 7, ε^t represents a stationary process and ζ^t is a random walk, specified as:

The null hypothesis is that of stationarity: H⁰: σ^2u = 0 or ζ^t is a constant. To determine whether the time series is stationary in levels, rather than testing trend stationarity, the test is conducted with a regression of y^t on an intercept.

In order to further overcome the low explanatory power of the ADF unit root test, Maddala and Kim (2000) suggest additionally using the DF-GLS test. The DF-GLS test is a modification of the ADF test and was proposed by Elliott, Rothenberg and Stock (1996). It determines whether a deterministic trend is present and de-trends the time series, which is explained by Enders (2010) as follows:

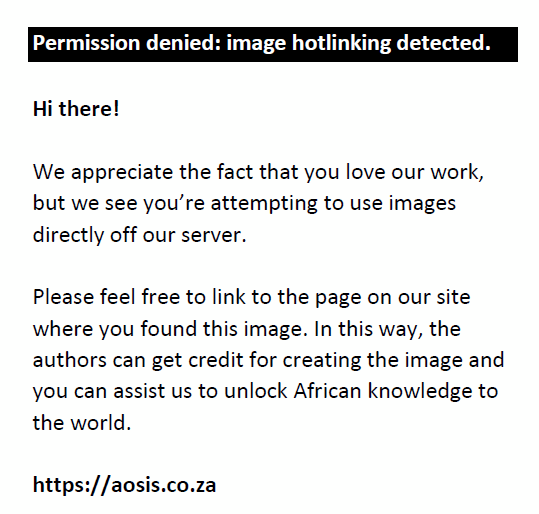
In Equation 9, y⁰ refers to the initial condition for period zero, a¹t is the deterministic trend component and ε^t is the pure noise component. The time series, y^t, is de-trended by regressing Equation 9 and obtaining the values of the series ε^t by subtracting the estimated values of y^t from the observed values in the time series. The de-trended series y^dt thus replaces y^t in the original ADF test equation and can be given as:

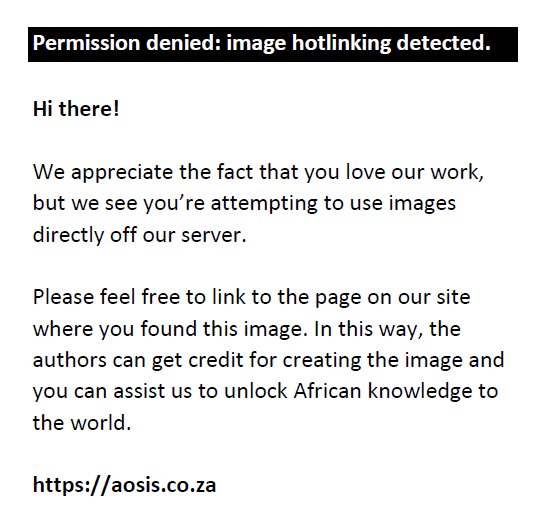
However, if the time series does not consist of a deterministic trend component there is still the possibility that the series requires fractional differencing in order to be stationary. This leads to the final phase that will determine the possibility of fractional integration and will conclude by determining the best differencing approach required to render a time series to the appropriate form of stationarity.

The GPH method estimates d by running the following ordinary least squares regression:

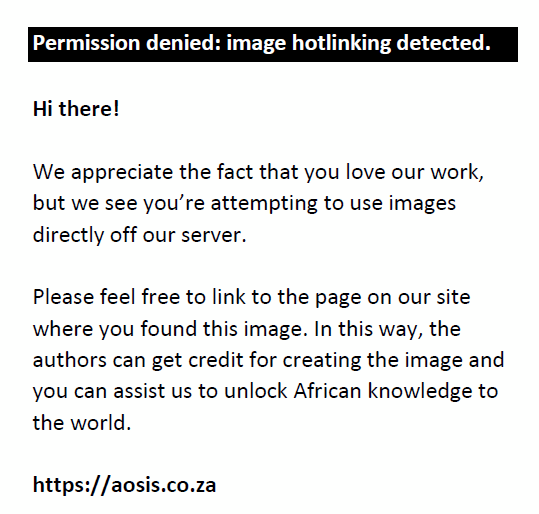
In Equation 11, j = 1, ..., n, 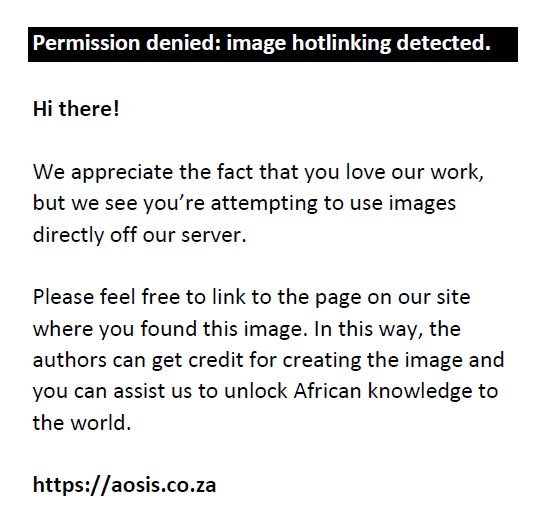, n = g(T ) < T and I(w^j) is the periodogram of X at frequencec w^j, which can be defined as:

According to Maddala and Kim (2000), the value of n should be set at n =and the estimated variance of d should be computed using the known variance of . The GPH method is also used to determine the presence of a unit root with the null hypothesis, H⁰: d = 0 and the alternative, H⁰: d ≠ 0. Further interpretations can also be summarised as follows: (1) if d = 0, the time series is covariance stationary; (2) if d is between 0 and 0.5 the time series remains covariance stationary; (3) if d falls between 0.5 and 1 the time series is no longer considered covariance stationary but the series is still mean reverting or has long memory; (4) if d ≥ 1 the series is non-stationary and shows no sign of mean reversion; (5) should the value of d be negative the interpretation remains unchanged except that the series has been over-differenced (Doornik et al. 2007; Gallegati 2008; Gil-Alana 2006; Styger, Viljoen & Van Vuuren 2008).

Finally, if the results from this process indicate that both first differencing and fractional differencing are significant, it is important to evaluate these differenced series with the d parameter to determine the most appropriate stationarity format. The differenced series with a d value closest to zero and most statistically significant will indicate the larger degree of stationarity (Gil-Alana 2006) and thus the required approach to render it to the appropriate form of stationarity.

The data were tested for the different forms of stationarity by means of the EViews 7 econometric software program and the open-source Gretl econometric software program was chosen to estimate the d parameter, with the GPH procedure, and to fractionally difference the data. The empirical results of the process discussed in Section 3 (also graphically depicted in Figure A1) are reported in full in Table A1 and also summarised in Table 1.

In determining the most appropriate form of stationarity for each variable, we will start with the evaluation of the entire sample period of the R157 as an example, to demonstrate the process as illustrated by Figure A1. Phase 1 starts by consulting the ADF tests, where all three variations (none, intercept, intercept & trend) do not reject the null hypothesis of a unit root. To endorse these results, the KPSS test is consulted, where the two variations (intercept, intercept & trend) confirm these results, with the presence of stationarity being rejected. The final step of phase 1 is to further verify if R157(1) is not stationary, which is confirmed by the two variations (intercept, intercept & trend) of the DF-GLS test. These results thus imply that R157(1) is not an I(0) series and does not possess a trend, but may be an I(1) or I(d) series, where d is a fraction. To confirm this possibility it is necessary to continue with phase 2 of the process.

Phase 2 commences with consultation of the ADF test, where all three variations reject the null hypothesis of a unit root. However, the results from the KPSS and DF-GLS do not confirm these findings, as both reject the null hypothesis for R157(1) to be stationary. These results imply that it is uncertain if R157(1) can be classified as an I(1) series, which raise the possibility of it being an I(d) series. This leads to phase 3, where again there is no agreement between the results found by the ADF, KPSS and DF-GLS tests. This implies that the d parameter must be consulted to determine the most appropriate form of stationarity. The differenced series with a d value closest to zero and most statistically significant will indicate the larger degree of stationarity (Gil-Alana 2006), which implies that R157(1) is an I(d) series and must be transformed accordingly before any econometric analysis can continue.

The rest of the variables under investigation were evaluated by following the same process as discussed above and illustrated in Figure A1; the results are summarised in Table 1. From Table 1 it is evident that each variable series can have a different requirement to render it stationary, with none of the variables being unvarying over the four sample sizes under investigation. For example, the pre-financial crisis and European debt crisis period of the ALSI, Dow Jones, FTSE and ZAR and/or USD exchange rate must be fractionally differenced in order to render them stationary, whereas the entire sample series of each of these variables must be first differenced in order to render them stationary. These findings highlight the importance of reconciling the different unit root and stationarity tests, as formulated by Figure A1, to determine the most appropriate form of stationarity for each variable, as the stationarity requirements can vary depending on the length of the sample size under investigation.

In addition, from the results reported in Table A1 and Table 1, it is also obvious that the choice of a specific sample period, especially if it incorporates the financial crisis or the European debt crisis, can have a significant effect on the form of stationarity. For example, the R157 required fractional differencing during the pre-financial crisis period but this changed during the financial crisis period, where evidence suggested it to be an I(1) series. However, this requirement changed again during the European crisis period, where the R157 once more required fractional differencing in order to render it stationary. Also, only the ANG required fractional differencing before the pre-financial crisis period, but exhibited I(0) behaviour during the financial crisis period and remained so during the European debt crisis period.

Furthermore, the results from Table A1 substantiate the possibility of over-differencing (if the d parameter is negative) if a series is to be transformed to the less appropriate form of stationarity. For example, the entire sample ANG(1) and smaller European debt crisis sample period of ANG illustrate the significant probability of being over-differenced if they are to be first differenced in order to be rendered stationary. Note that the Brent crude oil prices, FTSE and Dow Jones can present some difficulties when evaluating smaller sample sizes, especially during crisis periods. No conclusive evidence was found from the ADF, KPSS or DF-GLS, where the d parameter also reported negative estimates for both the possibility of fractional and first differencing, implying over-differencing. Though both d parameters were statistically insignificant, the first differencing process mostly reported a more statistically significant d parameter compared to fractional differencing, except Dow Jones(4) and Brent(4), which favoured fractional differencing more. Also, it is interesting to note that none of the variables under investigation required de-trending, though this does not imply that the presence of trend stationarity is impossible and must still be investigated accordingly.

Overall, there were several instances where the results from the ADF, KPSS and DF-GLS were not conclusive regarding which is the more appropriate stationarity (first differencing or fractional differencing) to apply. This highlighted the importance of consulting the d parameter to make a more informed decision, rather than only assuming that the data are I(1). Also, evidence suggests that the appropriate form of stationarity can vary, but emphasises the importance of considering a series to be fractionally differenced. In Table A1, 14 out of the 28 sample periods required fractional differencing, whereas 10 out of the 28 sample periods required first differencing to render them to the appropriate form of stationarity. The majority results clearly contradict the widely held view that the optimal form of stationarity can be accomplished by simply taking first differences, no matter what data one is working with. This belief is engrained in practice because of Nelson and Plosser’s (1982) findings, based on work they performed on US data mainly between 1860 and 1970. It is therefore improbable that the same results would apply for any other random dataset more than four decades later.

After applying this process, of rendering a time series to the appropriate form of stationarity, the following results were reported: (1) four time series were I(0) series, (2) 10 of the time series were first difference stationary, (3) a total of 14 time series were fractionally difference stationary and (4) more than half of the time series illustrated over-differencing after the first differencing process was applied. The results therefore confirm that it is imperative that the statistical properties of the specific data series be determined before deciding on the action to be taken. The assumption of most time series being first difference stationary cannot hold any longer, due to the risk of over-differencing a time series. If researchers practise due diligence and allow the statistical properties of a time series to lead them in rendering the series to the appropriate form of stationarity, the occurrence of over-differencing can be avoided and improved empirical results may be achieved.

Since the appropriate form of stationarity has such a great impact on time series econometric analysis, future research might be aimed at applying this methodology to a sliding window approach to determine the appropriate form of stationarity as the number of observations increase. A second avenue of research could further investigate the impact of the appropriate form of stationarity with the forecasting of a time series.

Asteriou, D. & Hall, S.G., 2007, Applied econometrics: A modern approach, Palgrave Macmillan, New York, NY.

Bekaert, G., Harvey, C.R., Lundblad, C.T. & Siegel, S., 2013, ‘The European Union, the Euro, and equity market integration’, Journal of Financial Economics 109(3), 583–603. http://dx.doi.org/10.1016/j.jfineco.2013.03.008

Blough, S.R., 1992, ‘The relationship between power and level for generic unit root tests in finite samples’, Journal of Applied Econometrics 7(3), 295–308. http://dx.doi.org/10.1002/jae.3950070306

Burke, S.P. & Hunter, J., 2005, Modelling non-stationary economic time series: A multivariate approach, Palgrave MacMillan, New York, NY.

Choi, I., 1994, ‘Residual-based tests for the null of stationarity with application to US macroeconomic time series’, Econometric Theory 10, 720–746. http://dx.doi.org/10.1017/S0266466600008744

Davies, R.B. & Harte, D.S., 1987. Tests for the Hurst effect, Biometrika Trust 74(1), 95–101. http://dx.doi.org/10.1093/biomet/74.1.95

DeJong, D.N., Nankervis, J.C., Savin, N.E. & Whiteman, C.H., 1992, ‘Integration versus trend stationary in time series’, Econometrica 60(2), 423–433. http://dx.doi.org/10.2307/2951602

Dickey, D.A. & Fuller, W.A., 1979, ‘Distribution of the estimators for autoregressive time series with a unit root’, Journal of the American Statistical Association 74(366), 427–431. http://dx.doi.org/10.2307/2286348

Dickey, D.A. & Fuller, W.A., 1981, ‘Likelihood ratio statistics for autoregressive time series with a unit root’, Econometrica 49(4), 1057–1072. http://dx.doi.org/10.2307/1912517

Doornik, J.A., Hendry, D.F., Arellano, M., Bond, S., Boswijk, H.P. & Ooms, M., 2007, Econometric modelling. PcGive, Vol 3. OxMetricsTM 5, Timberlake Consultants, London.

Elder, J. & Serletis, A., 2006, ‘On fractional integrating dynamics in the U.S. stock market’, Chaos, Solitons and Fractals 34(1), 777–781.

Elliott, G., Rothenberg, T.J. & Stock, J.H., 1996, ‘Efficient tests for an autoregressive unit root’, Econometrica 64(1), 813–836. http://dx.doi.org/10.2307/2171846

Enders, W., 2010, Applied econometric time series, Wiley, Hoboken, NJ.

Erfani, A. & Samimi, A.J., 2009, ‘Long memory forecasting of stock price index using a fractionally differenced ARMA model’, Journal of Applied Sciences Research 5(10), 1721–1731.

EViews, version 7, 2007, Quantitative Micro Software, Irvine, CA.

Fang, H., Kon, S.L. & Lai, M., 1994, ‘Fractal structure in currency futures price dynamics’, The Journal of Futures Markets 14(2), 169–181. http://dx.doi.org/10.1002/fut.3990140205

Fielitz, B.D., 1971, ‘Stationarity of random data: Some implications for the distribution of stock price changes’, Journal of Financial and Quantitative Analysis 6(3), 1025–1034. http://dx.doi.org/10.2307/2329918

Gallegati, M., 2008, ‘Wavelet analysis of share returns and aggregate economic activity’, Computational Statistics and Data Analysis 51(6), 3061–3074. http://dx.doi.org/10.1016/j.csda.2007.07.019

Geweke, J. & Porter-Hudak, A., 1983, ‘The estimation application of long-memory time series models’, Journal of Time Series Analysis 4(1), 221–238. http://dx.doi.org/10.1111/j.1467-9892.1983.tb00371.x

Gil-Alana, L.A., 2006, ‘Fractional integration in daily stock market indexes’, Review of Financial Economics 15, 28–48. http://dx.doi.org/10.1016/j.rfe.2005.02.003

Granger, C.W.J. & Newbold, P., 1974, ‘Spurious regressions in econometrics.’, Journal of Econometrics 2(2), 111–120. http://dx.doi.org/10.1016/0304-4076(74)90034-7

Hosking, J.R.M., 1981, ‘Fractional differencing’, Biometrika Trust 68(1), 1025–1034. http://dx.doi.org/10.1093/biomet/68.1.165

Hurst, H.E., 1951, ‘Long-term storage capacity of reservoirs’, Transactions of the American Society of Civil Engineers 116, 770–799.

Kwaitkowski, D., Phillips, P.C.B., Schmidt, P. & Shin, Y., 1992, ‘Testing the null hypothesis of stationarity against the alternative of a unit root’, Journal of Econometrics 54, 159–178. http://dx.doi.org/10.1016/0304-4076(92)90104-Y

Leybourne, S.J. & McCabe, B.P.M., 1994, ‘A consistent test for a unit root’, Journal of Business and Economic Statistics 12, 157–166.

Leybourne, S.J., McCabe, B.P.M. & Tremayne, A.R., 1996, ‘Can economic time series be differenced to stationarity?’, Journal of Business and Economic Statistics 14(4), 435–446.

Lo, A.W., 1991, ‘Long-term memory in stock market prices’, Econometrica 59(5), 1279–1313. http://dx.doi.org/10.2307/2938368

Maddala, G.S. & Kim, I.M., 2000, Unit roots, cointergration, and structural change, Cambridge, Cambridge.

Mandelbrot, B., 1972, ‘Statistical methodology for non-periodic cycles: From the covariance to R/S analysis’, Annals of Statistics 23(3), 1015–1028.

McGregor BFA, 2012, [database], data source, supplied by software.

Nelson, C. & Plosser, C., 1982, ‘Trends and random walks in macroeconomic time series models: Some evidence and implications’, Journal of Monetary Economics 10(2), 139–162. http://dx.doi.org/10.1016/0304-3932(82)90012-5

Park, J.Y., 1990, ‘Testing for unit roots and cointegration by variable addition’, Advances in Econometrics 8, 107–133.

Peng, C.K., Havlin, S., Stanley, H.E. & Goldberger, A.L., 1994, ‘Quantification of scaling exponents and crossover phenomena in non-stationary heartbeat time series’, Chaos 5(1), 82–87. http://dx.doi.org/10.1063/1.166141

Plosser, C.I. & Schwert, G.W., 1977, ‘Estimation of a non-invertible moving average process: The case of overdifferencing’, Journal of Econometrics 6(2), 199–224. http://dx.doi.org/10.1016/0304-4076(77)90015-X

Plosser, C.I. & Schwert, G.W., 1978, ‘Money, income and sunspots: Measuring economic relationships and the effects of differencing’, Journal of Monetary Economics 4(4), 637–660. http://dx.doi.org/10.1016/0304-3932(78)90021-1

Robinson, P., 1995, ‘Gaussian semi-parametric estimation of long range dependence’, The Annals of Statistics, 23(5), 1630–1661. http://dx.doi.org/10.1214/aos/1176324317

Saikkonen, P. & Luukkonen, R., 1993, ‘Testing for a moving average unit root in ARIMA models’, Journal of the American Statistical Association 88, 596–601. http://dx.doi.org/10.1080/01621459.1993.10476312

Sowell, F., 1990, ‘The fractional unit root distribution’, Econometrica 58(1), 495–505. http://dx.doi.org/10.2307/2938213

Styger, P., Viljoen, S. & Van Vuuren, G., 2008, ‘A triptuch on the USD-ZAR exchange rate dynamics’, in Proceeding of the 5th International Conference on Applied Financial Economics, Greece, July 03-05, 2008, pp. 334–344.

Tanaka, K., 1990, ‘Testing for a moving average unit root’, Econometric Theory 6, 433–444. http://dx.doi.org/10.1017/S0266466600005442

Van Greunen, J.A., Heymans, A., Van Heerden, C. & Van Vuuren, G.W., 2014, ‘The prominence of stationarity in time series forecasting’, Studies in Economics and Econometrics 38(1), 1–16.

Xiu, J. & Jin, Y., 2007, ‘Empirical study of ARFIMA model based on fractional differencing’, Physica A: Statistical Mechanics and its Applications 377(1), 138–154. http://dx.doi.org/10.1016/j.physa.2006.11.030

FIGURE 1A: The process of rendering a non-stationary time series stationary (Phases 1, 2 and 3).

FIGURE 1A (Continues...): The process of rendering a non-stationary time series stationary (Phases 1, 2 and 3).